
Jason J. Corso
| Snippets by Topic | |
| * | Active Clustering |
| * | Activity Recognition |
| * | Medical Imaging |
| * | Metric Learning |
| * | Semantic Segmentation |
| * | Video Segmentation |
| * | Video Understanding |
| Selected Project Pages | |
| * | Action Bank |
| * | LIBSVX: Supervoxel Library and Evaluation |
| * | Brain Tumor Segmentation |
| * | CAREER: Generalized Image Understanding |
| * | Summer of Code 2010: The Visual Noun |
| * | ACE: Active Clustering |
| * | ISTARE: Intelligent Spatiotemporal Activity Reasoning Engine |
| * | GBS: Guidance by Semantics |
| * | Semantic Video Summarization |
| Data Sets | |
| * | YouCook |
| * | Chen Xiph.org |
| * | UB/College Park Building Facades |
| Other Information | |
| * | Code/Data Downloads |
| * | List of Grants |
Coherent Interest Regions -- Coupled Segmentation and Correspondence
Collaborators: Greg Hager (JHU), Maneesh Dewan (Siemens)
 We study methods that attempt to integrate information from coherent
image regions to represent the image. Our novel sparse image
segmentation can be used to solve robust region correspondences and
therefore constrain the search for point correspondences. The
philosophy behind this work is that coherent image regions provide a
concise and stable basis for image representation: concise meaning that
the required space for representing the image is small, and stable
meaning that the representation is robust to changes in both viewpoint
and photometric imaging conditions.
In addition, we have proposed a subspace labeling technique for global
Image segmentation in a particular feature subspace is a fairly well
understood problem. However, it is well known that operating in only a
single feature subspace, e.g. color, texture, etc, seldom yields a good
segmentation for real images. However, combining information from
multiple subspaces in an optimal manner is a difficult problem to solve
algorithmically. We propose a solution that fuses contributions from
multiple feature subspaces using an energy minimization approach. For
each subspace, we compute a per-pixel quality measure and perform a
partitioning through the standard normalized cut algorithm. To fuse the
subspaces into a final segmentation, we compute a subspace label for
every pixel. The labeling is computed through the graph-cut energy
minimization framework proposed by Boykov et al. Finally, we combine
the initial subspace segmentation with the subspace labels obtained from
the energy minimization to yield the final segmentation.
Publications:
We study methods that attempt to integrate information from coherent
image regions to represent the image. Our novel sparse image
segmentation can be used to solve robust region correspondences and
therefore constrain the search for point correspondences. The
philosophy behind this work is that coherent image regions provide a
concise and stable basis for image representation: concise meaning that
the required space for representing the image is small, and stable
meaning that the representation is robust to changes in both viewpoint
and photometric imaging conditions.
In addition, we have proposed a subspace labeling technique for global
Image segmentation in a particular feature subspace is a fairly well
understood problem. However, it is well known that operating in only a
single feature subspace, e.g. color, texture, etc, seldom yields a good
segmentation for real images. However, combining information from
multiple subspaces in an optimal manner is a difficult problem to solve
algorithmically. We propose a solution that fuses contributions from
multiple feature subspaces using an energy minimization approach. For
each subspace, we compute a per-pixel quality measure and perform a
partitioning through the standard normalized cut algorithm. To fuse the
subspaces into a final segmentation, we compute a subspace label for
every pixel. The labeling is computed through the graph-cut energy
minimization framework proposed by Boykov et al. Finally, we combine
the initial subspace segmentation with the subspace labels obtained from
the energy minimization to yield the final segmentation.
Publications:
 We study methods that attempt to integrate information from coherent
image regions to represent the image. Our novel sparse image
segmentation can be used to solve robust region correspondences and
therefore constrain the search for point correspondences. The
philosophy behind this work is that coherent image regions provide a
concise and stable basis for image representation: concise meaning that
the required space for representing the image is small, and stable
meaning that the representation is robust to changes in both viewpoint
and photometric imaging conditions.
In addition, we have proposed a subspace labeling technique for global
Image segmentation in a particular feature subspace is a fairly well
understood problem. However, it is well known that operating in only a
single feature subspace, e.g. color, texture, etc, seldom yields a good
segmentation for real images. However, combining information from
multiple subspaces in an optimal manner is a difficult problem to solve
algorithmically. We propose a solution that fuses contributions from
multiple feature subspaces using an energy minimization approach. For
each subspace, we compute a per-pixel quality measure and perform a
partitioning through the standard normalized cut algorithm. To fuse the
subspaces into a final segmentation, we compute a subspace label for
every pixel. The labeling is computed through the graph-cut energy
minimization framework proposed by Boykov et al. Finally, we combine
the initial subspace segmentation with the subspace labels obtained from
the energy minimization to yield the final segmentation.
Publications:
We study methods that attempt to integrate information from coherent
image regions to represent the image. Our novel sparse image
segmentation can be used to solve robust region correspondences and
therefore constrain the search for point correspondences. The
philosophy behind this work is that coherent image regions provide a
concise and stable basis for image representation: concise meaning that
the required space for representing the image is small, and stable
meaning that the representation is robust to changes in both viewpoint
and photometric imaging conditions.
In addition, we have proposed a subspace labeling technique for global
Image segmentation in a particular feature subspace is a fairly well
understood problem. However, it is well known that operating in only a
single feature subspace, e.g. color, texture, etc, seldom yields a good
segmentation for real images. However, combining information from
multiple subspaces in an optimal manner is a difficult problem to solve
algorithmically. We propose a solution that fuses contributions from
multiple feature subspaces using an energy minimization approach. For
each subspace, we compute a per-pixel quality measure and perform a
partitioning through the standard normalized cut algorithm. To fuse the
subspaces into a final segmentation, we compute a subspace label for
every pixel. The labeling is computed through the graph-cut energy
minimization framework proposed by Boykov et al. Finally, we combine
the initial subspace segmentation with the subspace labels obtained from
the energy minimization to yield the final segmentation.
Publications:
| [1] | J. J. Corso and G. D. Hager. Image Description with Features that Summarize. Computer Vision and Image Understanding, 113:446-458, 2009. [ bib | .pdf ] |
| [2] | J. J. Corso and G. D. Hager. Coherent Regions for Concise and Stable Image Description . In Proceedings of IEEE Conference on Computer Vision and Pattern Recognition, volume 2, pages 184-190, 2005. [ bib | .pdf ] |
| [3] | J. J. Corso, M. Dewan, and G. D. Hager. Image Segmentation Through Energy Minimization Based Subspace Fusion. In Proceedings of 17th International Conference on Pattern Recogntion (ICPR 2004), 2004. [ bib | .pdf ] |
| [4] | J. J. Corso, M. Dewan, and G. D. Hager. Image Segmentation Through Energy Minimization Based Subspace Fusion. Technical Report CIRL-TR-04-01, The Johns Hopkins University, 2004. [ bib | .pdf ] |
Interest Region Operator
The philosophy behind this work is that coherent image regions
provide a concise and stable basis for image
representation: concise meaning that the required space for representing
the image is small, and stable meaning that the representation is robust
to changes in both viewpoint and photometric imaging conditions. On
this webpage, we provide a brief overview into the work and refer the
reader to the papers for more detailed
information. Please contact us with any further
questions.
Discussion
We are interested in the problems of scene retrieval and scene mapping.
Our underlying approach to solving these problems is region-based: a
coherent region is a connected set of relatively homogeneous pixels in
the image. For example, a red ball would project to a red circle in the
image, or the stripes on a zebra's back would be coherent
vertical stripes.
Our approach is a "middle ground" between the two popular approaches in
image description: local region descriptors (e.g. Schmid and Mohr [PAMI,
1997] and Lowe [IJCV, 2004]) and global image segmentation (e.g. Malik
et al [ICCV, 1999; PAMI, 2002]). We focus on creating interest
operators for coherent regions and robust, but concise descriptors for
the regions. To that end, we develop a sparse grouping algorithm that
functions in parallel over several scalar image projections (feature
spaces). We use kernel-based optimization techniques to create a
continuous scale-space of the coherent regions. The optimization
evaluates both the size (large regions are expected to be stable over
widely disparate views) and the coherency (e.g. similar color, texture,
etc). The descriptor for a given region is simply a vector of
kernel-weighted means over the feature spaces. The description is
concise, it is stable under drastic changes in viewpoint, and it is
insensitive to photometric changes (given insensitive feature spaces).
We provide a brief explanation and some examples for the parts of this
work: detection and matching.
Detection and Description
We represent by a Gaussian kernel to facilitate continuous optimization
techniques in detect (and registration). The kernels are applied to
scalar projections of the image; the intuition is that various
projection functions will map a region of consistent image content to a
homogeneous image patch in the scalar field. Below, we show an image,
its projection under neighborhood variance and the extracted regions.
(The regions are drawn as ellipses corresponding to 3 standard
deviations of the kernel.)

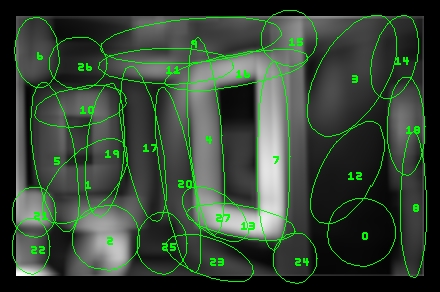
Here, we show the same image and its complete region-representation in color space.

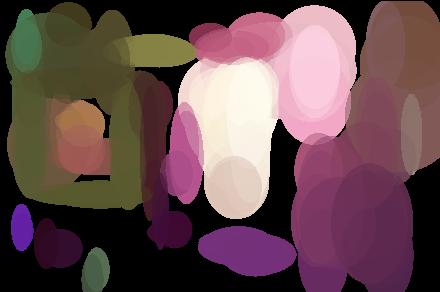
We describe each region by the vector of kernel-weighted means under all projections that were used during detection. This representation is both concise and stable. We show a table comparing its memory footprint versus two other methods (Lowe's SIFT and Carson, Malik et al.'s Blobworld). These results are for our dataset (discussed below). We are grateful to both of the other groups for providing their source code/binaries which facilitated this analysis.
Next, we show empirical evidence that our approach is stable under gross
viewpoint changes. We distort the input image by various affine
transformations and detect the regions. From the figure below, we can see
that roughly the same regions are detected. Note, that our current
kernel is axis-aligned; in order to make the kernel fully
affine-invariant we would have to add a 5 parameter for rotation and a 6
(a pre-kernel image warp) for image skew.



Here, we show the same image and its complete region-representation in color space.

We describe each region by the vector of kernel-weighted means under all projections that were used during detection. This representation is both concise and stable. We show a table comparing its memory footprint versus two other methods (Lowe's SIFT and Carson, Malik et al.'s Blobworld). These results are for our dataset (discussed below). We are grateful to both of the other groups for providing their source code/binaries which facilitated this analysis.
| Average Number of Elements | Size per element (in Words) | Average size (in Words) | |
| Our Technique | 159 | 5 | 797 |
| Blobworld | 9 | 239 | 2151 |
| SIFT | 695 | 32 | 22260 |

Matching
Currently, we use a simple nearest neighbor analysis on the regions'
feature vector to measure similarity and voting (over the whole
database) for image retrieval. Below is an example of both a positive
and negative match.
To compare our approach to the other two approaches mentioned earlier, we performed an image retrieval experiment on a set of 48 images taken of the same, indoor scene. All images can be found here. Two images are considered matching if there is an pixel-area overlap. We use the standard precision (fraction of true-positive matches from all retrieved) and recall (fraction of matching images retrieved against the total possible matching images in the database). A sample of the database is below.

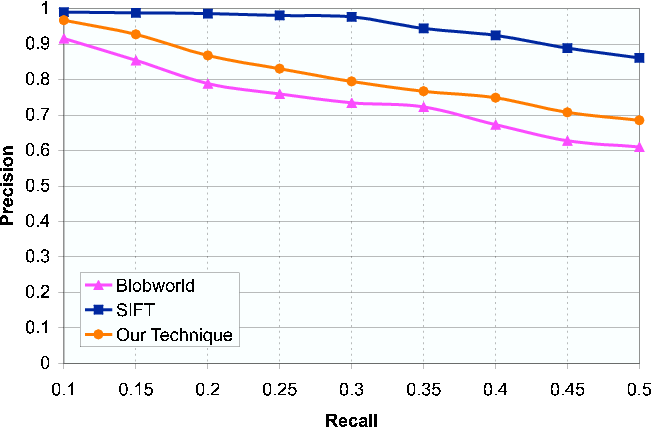
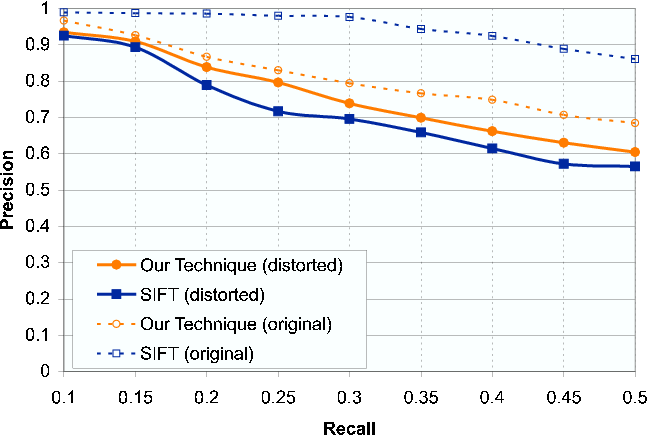
We see the SIFT performs the best for the standard retrieval experiment. This results agrees with those found by Mikolajczyk and Schmid (CVPR, 2003). Note that SIFT is storing substantially more information that both our method and Blobworld. Next, we compare out method to SIFT after distorting the query images drastically by halving the aspect ratio. We find that our method is very robust to such a change and surpasses SIFT in the precision-recall plot.
Positive
|
Negative
|
To compare our approach to the other two approaches mentioned earlier, we performed an image retrieval experiment on a set of 48 images taken of the same, indoor scene. All images can be found here. Two images are considered matching if there is an pixel-area overlap. We use the standard precision (fraction of true-positive matches from all retrieved) and recall (fraction of matching images retrieved against the total possible matching images in the database). A sample of the database is below.


We see the SIFT performs the best for the standard retrieval experiment. This results agrees with those found by Mikolajczyk and Schmid (CVPR, 2003). Note that SIFT is storing substantially more information that both our method and Blobworld. Next, we compare out method to SIFT after distorting the query images drastically by halving the aspect ratio. We find that our method is very robust to such a change and surpasses SIFT in the precision-recall plot.

Subspace Fusion for Global Segmentation
We have proposed a subspace labeling technique for global Image
segmentation in a particular feature subspace is a fairly well understood
problem. However, it is well known that operating in only a single feature
subspace, e.g. color, texture, etc, seldom yields a good segmentation for
real images. However, combining information from multiple subspaces in an
optimal manner is a difficult problem to solve algorithmically. We propose a
solution that fuses contributions from multiple feature subspaces using an
energy minimization approach. For each subspace, we compute a per-pixel
quality measure and perform a partitioning through the standard normalized cut
algorithm. To fuse the subspaces into a final segmentation, we compute a
subspace label for every pixel. The labeling is computed through the graph-cut
energy minimization framework proposed by Boykov et al. Finally, we
combine the initial subspace segmentation with the subspace labels
obtained from the energy minimization to yield the final segmentation.
Examples of the algorithms being studied follow:






|